In 1976, Whitfield Diffie and Martin Hellman wrote a paper describing a cryptographic technique to exchange a shared secret publicly. Here’s a link to the original paper. It is an interesting historical moment that has shaped the internet and modern computing as we know it. It is definitely worth a read. I’ll also link a YouTube video for visual learners. (In fact, I would watch the video first, then checkout the paper).
But before we get into the Diffie-Hellman key exchange scheme, we need to define couple of key terms:
Asymmetric encryption: aka public key cryptography. In this scheme, public keys are used to encrypt messages and private keys are used to decode messages. Wikipedia (Public Key Cryptography)
Symmetric encryption: a cryptographic method where both communicating parties share a private key that provides both encryption and decryption. Wikipedia (Symmetric Key Algorithm)
While symmetric encryption is more efficient at scale, it presents a dilemma: how can two entities exchange a private key over the internet securely? Enter the Diffie-Hellman key exchange scheme. Diffie-Hellman key exchange is an asymmetric scheme that allows two machines to establish a connection where both entities share a private key.
Like the video, we will use colors to illustrate how Diffie-Hellman allows us to exchange a private key securely. In reality, these colors represent numbers and mathematical functions.
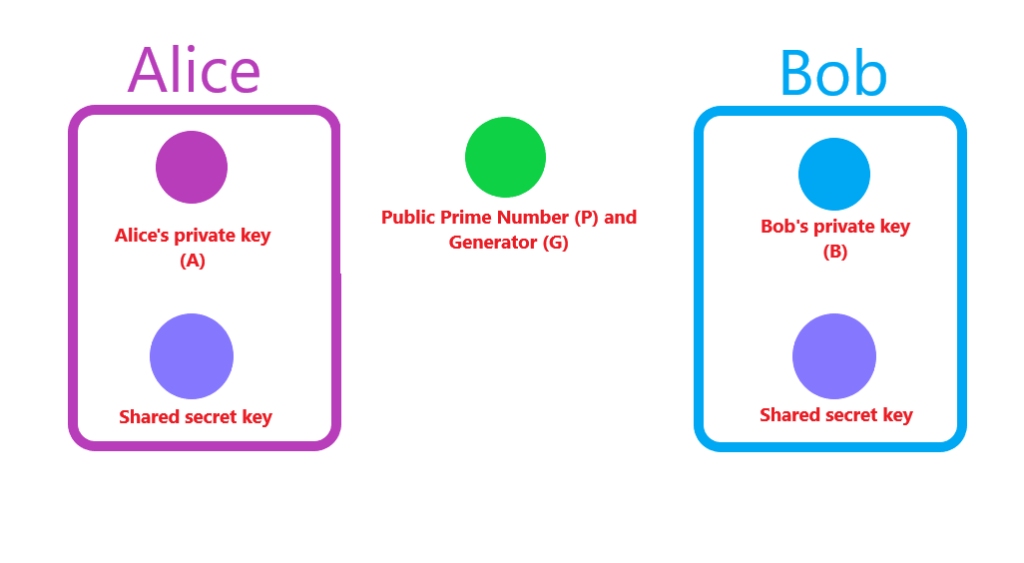
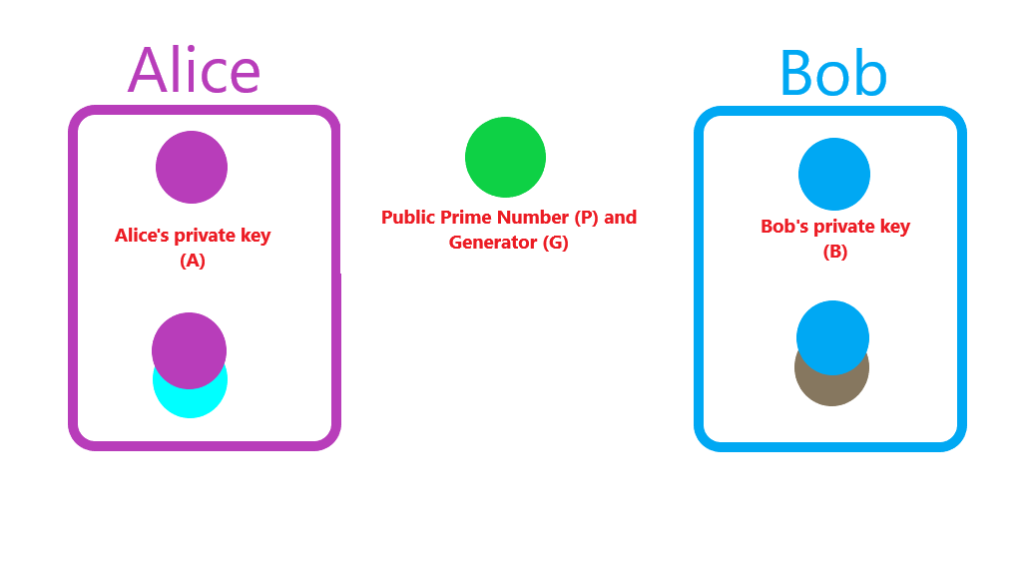
Meet Alice and Bob.
Both Alice and Bob have private keys that are securely stored away from the general public. The space in between Alice and Bob represents the public domain.
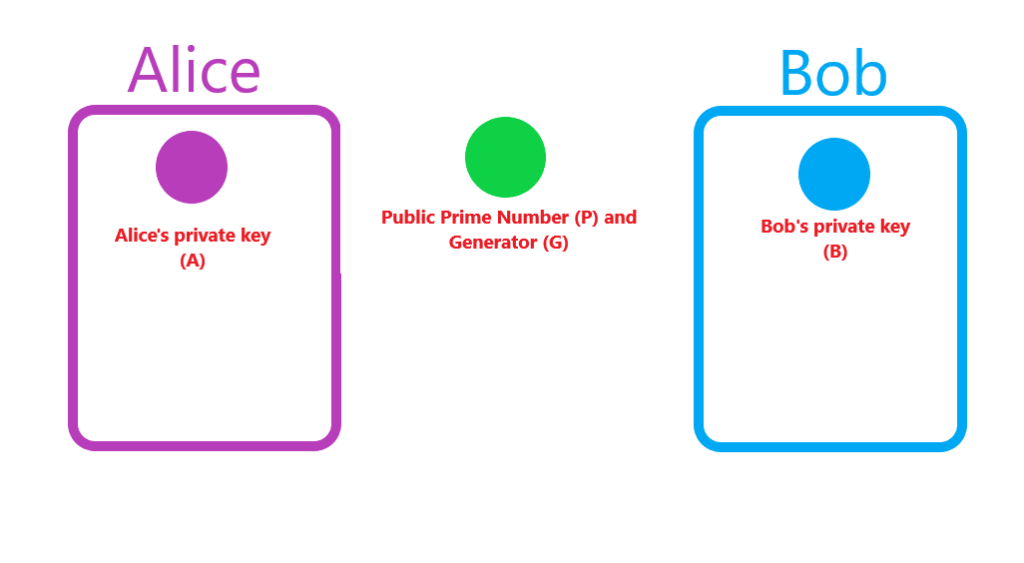
First, Alice and Bob agree on a prime number (P) and a generator number (G). These values are used in combination with their respective private key to produce a public key. Now, both Alice and Bob have a private/public key pair.
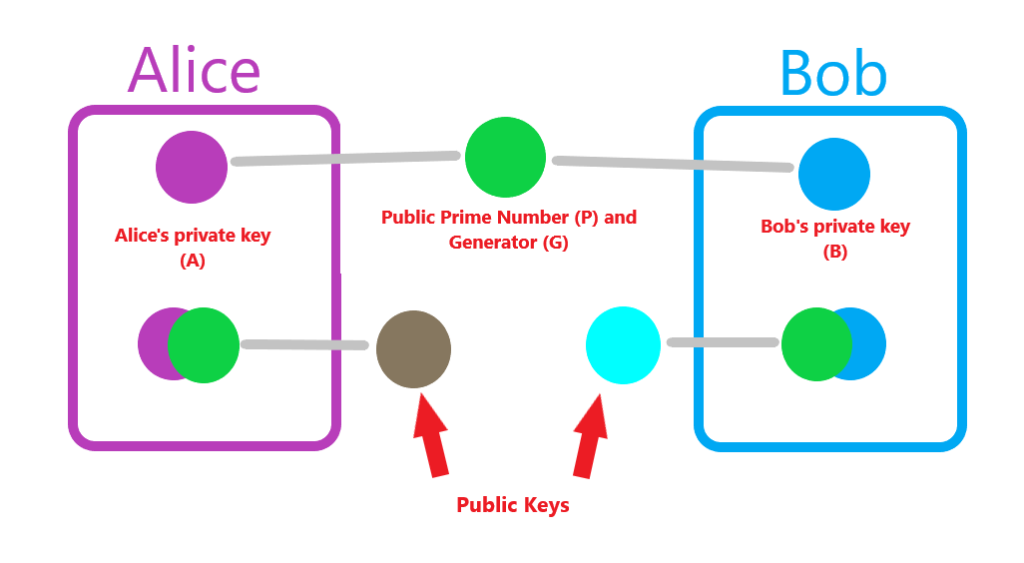
Now Alice sends her public key to Bob, and Bob sends his public key to Alice.
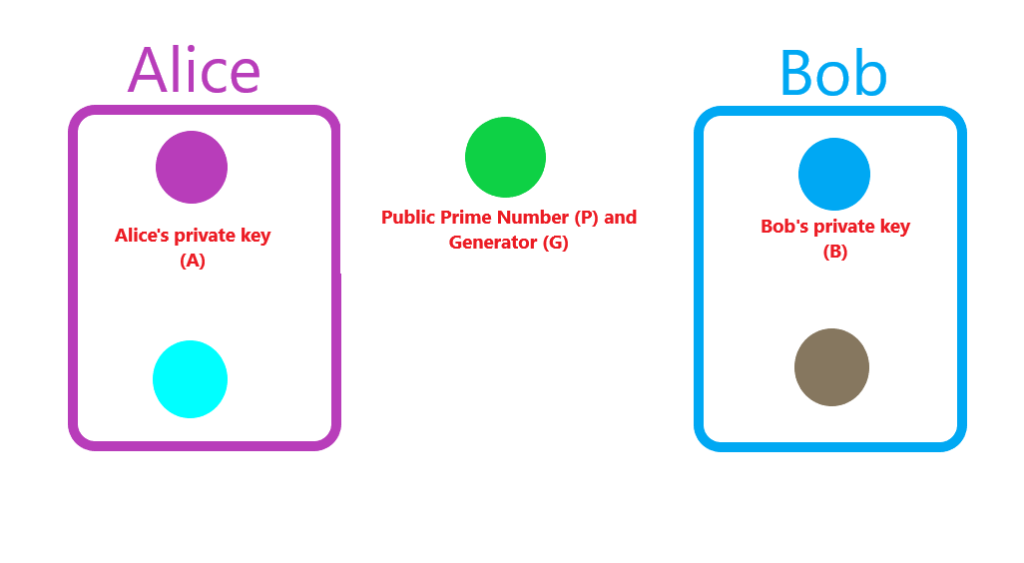
Here’s where the magic happens. Alice uses her private key and Bob’s public key to produce a shared secret key. The same shared secret key that Bob will create by using his private key and Alice’s public key.
Let’s suppose I intercepted every piece of data exchanged between Alice and Bob before the shared secret key was created. Remember that neither Alice’s nor Bob’s private key are ever exchanged. Alice and Bob generate a public key using an agreed upon prime number and generator (Let’s call this combination G). Alice combines this with her private key (we’ll call this AG) and sends it unencrypted to Bob. Bob does the same and sends his public key (BG) to Alice. Now I know the value of G, AG, and BG.
The shared secret is ABG. Alice derives this from her private key and the public key that Bob shared with her and Bob does the same with his private key and Alice’s public key. So even if I captured every piece of plain-text data passed between Alice and Bob, I still could not generate the shared secret key.